El movimiento de un fluido real es muy complejo. Para simplificar su descripción consideraremos el comportamiento de un fluido ideal cuyas características son las siguientes:
1.-Fluido no viscoso. Se desprecia la fricción interna entre las distintas partes del fluido
2.-Flujo estacionario. La velocidad del fluido en un punto es constante con el tiempo
3.-Fluido incompresible. La densidad del fluido permanece constante con el tiempo
4.-Flujo irrotacional. No presenta torbellinos, es decir, no hay momento angular del fluido respecto de cualquier punto.
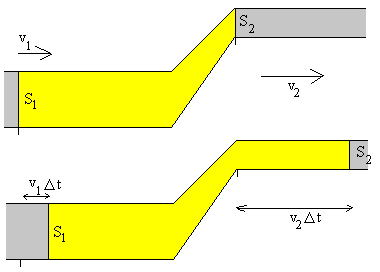
Consideremos una porción de fluido en color amarillo en la figura, el instante inicial t y en el instante t+Dt.
En un intervalo de tiempo Dt la sección S1 que limita a la porción de fluido en la tubería inferior se mueve hacia la derecha Dx1=v1Dt. La masa de fluido desplazada hacia la derecha es Dm1=r·S1Dx1=rS1v1Dt.
Análogamente, la sección S2 que limita a la porción de fluido considerada en la tubería superior se mueve hacia la derecha Dx2=v2Dt. en el intervalo de tiempo Dt. La masa de fluido desplazada es Dm2=r S2v2 Dt. Debido a que el flujo es estacionario la masa que atraviesa la sección S1 en el tiempo Dt, tiene que ser igual a la masa que atraviesa la sección S2 en el mismo intervalo de tiempo. Luego
Esta relación se denomina ecuación de continuidad.
En la figura, el radio del primer tramo de la tubería es el doble que la del segundo tramo, luego la velocidad del fluido en el segundo tramo es cuatro veces mayor que en el primero.
Ejemplo:
Cuando se abre poco a poco un grifo, se forma un pequeño chorro de agua, un hilo cuyo radio va disminuyendo con la distancia al grifo y que al final, se rompe formando gotas.
La ecuación de continuidad nos proporciona la forma de la superficie del chorrito de agua que cae del grifo, tal como apreciamos en la figura.
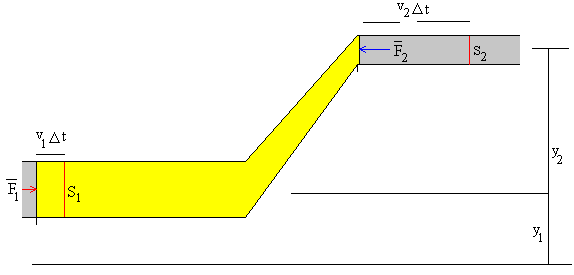
El elemento de masa Dm se puede expresar como Dm=r S2v2Dt=r S1v1Dt= r DV
Comparando la situación inicial en el instante t y la situación final en el instante t+Dt. Observamos que el elemento Dm incrementa su altura, desde la altura y1 a la altura y2
La fuerza F1 se desplaza Dx1=v1Dt. La fuerza y el desplazamiento son del mismo signo
La fuerza F2 se desplaza Dx2=v2 Dt. La fuerza y el desplazamiento son de signos contrarios.
Wext=Ef-Ei=(Ek+Ep)f-(Ek+Ep)i=DEk+DEp
Simplificando el término DV y reordenando los términos obtenemos la ecuación de Bernoulli
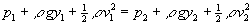
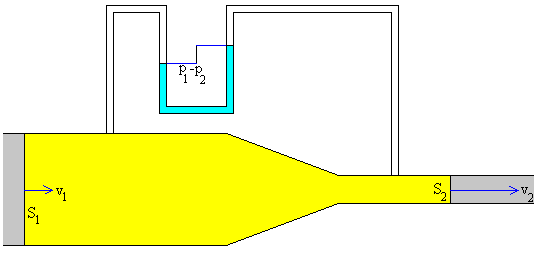
Cuando el desnivel es cero, la tubería es horizontal. Tenemos entonces, el denominado tubo de Venturi, cuya aplicación práctica es la medida de la velocidad del fluido en una tubería. El manómetro mide la diferencia de presión entre las dos ramas de la tubería.
La ecuación de continuidad se escribe
v1S1=v2S2
Que nos dice que la velocidad del fluido en el tramo de la tubería que tiene menor sección es mayor que la velocidad del fluido en el tramo que tiene mayor sección. Si S1>S2, se concluye que v1<v2.
La en la ecuación de Bernoulli con y1=y2
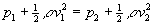
Como la velocidad en el tramo de menor sección es mayor, la presión en dicho tramo es menor.
Si v1<v2 se concluye que p1>p2 El líquido manométrico desciende por el lado izquierdo y asciende por el derecho.
Podemos obtener las velocidades v1 y v2 en cada tramo de la tubería a partir de la lectura de la diferencia de presión p1-p2 en el manómetro.
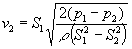
1.-Fluido no viscoso. Se desprecia la fricción interna entre las distintas partes del fluido
2.-Flujo estacionario. La velocidad del fluido en un punto es constante con el tiempo
3.-Fluido incompresible. La densidad del fluido permanece constante con el tiempo
4.-Flujo irrotacional. No presenta torbellinos, es decir, no hay momento angular del fluido respecto de cualquier punto.
Ecuación de la continuidad

Consideremos una porción de fluido en color amarillo en la figura, el instante inicial t y en el instante t+Dt.
En un intervalo de tiempo Dt la sección S1 que limita a la porción de fluido en la tubería inferior se mueve hacia la derecha Dx1=v1Dt. La masa de fluido desplazada hacia la derecha es Dm1=r·S1Dx1=rS1v1Dt.
Análogamente, la sección S2 que limita a la porción de fluido considerada en la tubería superior se mueve hacia la derecha Dx2=v2Dt. en el intervalo de tiempo Dt. La masa de fluido desplazada es Dm2=r S2v2 Dt. Debido a que el flujo es estacionario la masa que atraviesa la sección S1 en el tiempo Dt, tiene que ser igual a la masa que atraviesa la sección S2 en el mismo intervalo de tiempo. Luego
| v1S1=v2S2 |
Esta relación se denomina ecuación de continuidad.
En la figura, el radio del primer tramo de la tubería es el doble que la del segundo tramo, luego la velocidad del fluido en el segundo tramo es cuatro veces mayor que en el primero.
Ejemplo:
Cuando se abre poco a poco un grifo, se forma un pequeño chorro de agua, un hilo cuyo radio va disminuyendo con la distancia al grifo y que al final, se rompe formando gotas.
La ecuación de continuidad nos proporciona la forma de la superficie del chorrito de agua que cae del grifo, tal como apreciamos en la figura.
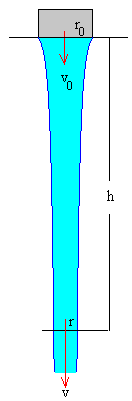 | La sección trasversal del chorro de agua cuando sale del grifo es S0, y la velocidad del agua es v0. Debido a la acción de la gravedad la velocidad v del agua se incrementa. A una distancia h del grifo la velocidad es Aplicando la ecuación de continuidad 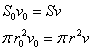 Despejamos el radio r del hilo de agua en función de la distancia h al grifo. 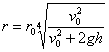 |
Ecuación de Bernoulli
Evaluemos los cambios energéticos que ocurren en la porción de fluido señalada en color amarillo, cuando se desplaza a lo largo de la tubería. En la figura, se señala la situación inicial y se compara la situación final después de un tiempo Dt. Durante dicho intervalo de tiempo, la cara posterior S2 se ha desplazado v2 Dt y la cara anterior S1 del elemento de fluido se ha desplazado v1Dt hacia la derecha.
El elemento de masa Dm se puede expresar como Dm=r S2v2Dt=r S1v1Dt= r DV
Comparando la situación inicial en el instante t y la situación final en el instante t+Dt. Observamos que el elemento Dm incrementa su altura, desde la altura y1 a la altura y2
- La variación de energía potencial es DEp=Dm·gy2-Dm·gy1=r DV·(y2-y1)g
- La variación de energía cinética es DEk =
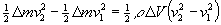
La fuerza F1 se desplaza Dx1=v1Dt. La fuerza y el desplazamiento son del mismo signo
La fuerza F2 se desplaza Dx2=v2 Dt. La fuerza y el desplazamiento son de signos contrarios.
- El trabajo de las fuerzas exteriores es Wext=F1 Dx1- F2 Dx2=(p1-p2) DV
Wext=Ef-Ei=(Ek+Ep)f-(Ek+Ep)i=DEk+DEp
Simplificando el término DV y reordenando los términos obtenemos la ecuación de Bernoulli
Efecto Venturi

Cuando el desnivel es cero, la tubería es horizontal. Tenemos entonces, el denominado tubo de Venturi, cuya aplicación práctica es la medida de la velocidad del fluido en una tubería. El manómetro mide la diferencia de presión entre las dos ramas de la tubería.
La ecuación de continuidad se escribe
v1S1=v2S2
Que nos dice que la velocidad del fluido en el tramo de la tubería que tiene menor sección es mayor que la velocidad del fluido en el tramo que tiene mayor sección. Si S1>S2, se concluye que v1<v2.
La en la ecuación de Bernoulli con y1=y2
Como la velocidad en el tramo de menor sección es mayor, la presión en dicho tramo es menor.
Si v1<v2 se concluye que p1>p2 El líquido manométrico desciende por el lado izquierdo y asciende por el derecho.
Podemos obtener las velocidades v1 y v2 en cada tramo de la tubería a partir de la lectura de la diferencia de presión p1-p2 en el manómetro.

Amigo Jon Ezquerro, tengo una duda acerca del efecto venturi. Como bien se sabe un fluido siempre se moverá de zonas de altas a bajas presiones. Ahora bien, lo que no entiendo es porque en este caso el fluido va de una zona de baja presión a otra de mayor presión. Si me puedes explicar eso me harías un gran favor. Gracias.
ResponderEliminar